Seri-paralel bağlantıda ortaya çıkan direncin hesaplanması

Kavramlar ve formüller

Seri paralel veya karışık bağlantı, üç veya daha fazla direncin karmaşık bir bağlantısıdır. Karışık bir bağlantının ortaya çıkan direnci, seri ve paralel bağlantılardaki dirençlerin hesaplanması için formüller kullanılarak aşamalar halinde hesaplanır.

Örnekleri

1. Şekil 2'deki şemaya göre üç direncin seri-paralel bağlantısını hesaplayın. 1.

İlk olarak, paralel bağlı dirençler r2 ve r3'ü ortaya çıkan direnç r (2-3) ile değiştirin:

r (2-3) = (r2 ∙ r3) / (r2 + r3) = (10 ∙ 20) / 30 = 6,6 ohm.

Tüm devrenin ortaya çıkan direnci r = r1 + r (2-3) = 5 + 6,6 = 11,6 ohm'dur.

Pirinç. 1.

2. Açık ve kapalı durumlarda devreden (Şekil 2) hangi akım akar? bıçak anahtarı P? Her iki durumda da direnç r2 üzerindeki voltaj nasıl değişir?

Pirinç. 2.

a) Anahtar açık. Seri bağlı dirençler r1 ve r2'nin bileşke direnci

r(1-2) = r1 + r2 = 25 ohm.

Akım I (1-2) = U / r (1-2) = 100/25 = 4 A.

Direnç r2 boyunca voltaj düşüşü

U2 = ben (1-2) ∙ r2 = 4 ∙ 5 = 20 V.

b) Anahtar kapalıdır. Paralel bağlı r1 ve r3 dirençlerinin bileşke direnci

r (1-3) = (r1 ∙ r3) / (r1 + r3) = (20 ∙ 10) / (20 + 10) = 200/30 = 6,6 ohm.

Tüm devrenin toplam direnci r = r (1-3) + r2 = 6,6 + 5 = 11,6 ohm'dur.

Akım ben = U / r = 100 / 11,6 = 8,62 A.

Bu durumda r2 direnci üzerindeki voltaj düşüşü şuna eşittir: U2 = I ∙ r2 = 8,62 ∙ 5 = 43,25 V.

İkinci durumda, paralel direnç R3'ün bağlanması sonucunda akım arttı. Daha fazla akım daha fazlasını yaratır gerilim düşümü r2 direncinde.

3. Ne olmalı? ek direnç rd, böylece 120 V voltaj ve 0,2 A akım için paralel bağlanan iki lamba, U = 220 V voltajlı bir ağa bağlanabilir (Şekil 3)?

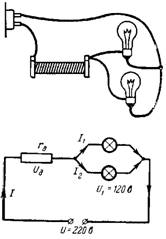
Pirinç. 3.

Lambalardaki voltaj 120 V'a eşit olmalıdır. Kalan voltaj (100 V) ek direnç rd'ye düşer. Direnç rd'den iki lamba akımı I = 0,4 A akar.

Ohm yasasına göre rd = Ud / I = 100 / 0.4 = 250 Ohm.

4. 1,2 V filamanlı ve 0,025 ve 0,05 A filaman akımına sahip elektronik lambalar, 4,5 V DC voltaj kaynağına seri olarak bağlanır. Ek direnç rd ve ne olmalıdır paralel direnç (şant) daha düşük filaman akımına sahip bir lambaya mı (şek. 4)?

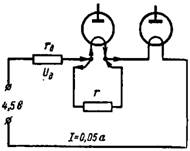
Pirinç. 4.

Devredeki dirençler ikinci lambanın filaman akımı I = 0,05 A olacak şekilde seçilmelidir. Elektronik lambaların filamanındaki gerilim 1,2 + 1,2 = 2,4 V olacaktır. Bu değeri akü geriliminden çıkarırsak, ek direnç rd üzerindeki voltaj düşüşünün değerini alın: Ud = 4,5-2,4 = 2,1 V.

Bu nedenle, ek direnç rd = (Ud) / I = 2,1 / 0,05 = 42 Ohm.

İlk vakum tüpünün filamanından 0,05 A'lik bir filaman akımı geçmemelidir. Bu akımın yarısı (0.05-0.025 = 0.025 A) r şöntünden geçmelidir. Şönt voltajı, lambanın filamanı ile aynıdır, yani 1,2 V. Bu nedenle, şönt direnci: r = 1,2 / 0,025 = 48 Ohm'dur.

5. Şekil 2'deki devrede ortaya çıkan devre direnci ve içindeki akım nedir? 5?

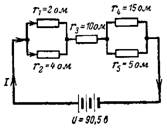
Pirinç. 5.

İlk olarak, paralel bağlı dirençlerin ortaya çıkan direncini belirleyelim:

r (1-2) = (r1 ∙ r2) / (r1 + r2) = (2 ∙ 4) / (2 + 4) = 8/6 = 1,3 ohm;

r (4-5) = (r4 ∙ r5) / (r4 + r5) = (15 ∙ 5) / (15 + 5) = 75/20 = 3,75 ohm.

Ortaya çıkan devre direnci:

r = r (1-2) + r3 + r (4-5) = 1,3 + 10 + 3,75 = 15,05 ohm.

U = 90,5 V geriliminde ortaya çıkan akım

ben = U / r = 90,5 / 15,05 = 6 A.

6. Şekil 2'deki devrede karmaşık bir seri-paralel bağlantının ortaya çıkan direncini hesaplayın. 6. Ortaya çıkan I akımını, I4 akımını ve r1 direnci boyunca voltaj düşüşünü hesaplayın.

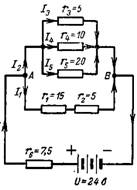
Pirinç. 6.

Paralel bağlı dirençlerin bileşke iletkenliği

1 / r (3-4-5) = 1 / r3 + 1 / r4 + 1 / r5 = 1/5 + 1/10 + 1/20 = 7/20 sim;

r (3-4-5) = 20/7 = 2,85 ohm.

r1 ve r2'nin devre direnci:

r(1-2) = r1 + r2 = 15 + 5 = 20 ohm.

A ve B noktaları arasında ortaya çıkan iletkenlik ve direnç sırasıyla eşittir: 1 / rAB = 1 / r (3-4-5) + 1 / r (1-2) = 7/20 + 1/20 = 8/20 sim ; rAB = 20/8 = 2,5 ohm.

Tüm devrenin ortaya çıkan direnci r = rAB + r6 = 2,5 + 7,5 = 10 ohm'dur.

Ortaya çıkan akım I = U / r = 24/10 = 2,4 A'dır.

A ve B noktaları arasındaki voltaj, kaynak voltajı U eksi direnç r6 üzerindeki voltaj düşüşüne eşittir.

UAB = UI ∙ r6 = 24-(2,4 ∙ 7,5) = 6V.

Direnç r4 bu gerilime bağlıdır, dolayısıyla içinden geçen akım şuna eşit olacaktır:

I4 = UAB / r4 = 6/10 = 0,6A.

Dirençler r1 ve r2, ortak bir UAB voltaj düşüşüne sahiptir, dolayısıyla r1'den geçen akım:

I1 = UAB / r (1-2) = 6/20 = 0,3 A.

Direnç r1 boyunca voltaj düşüşü

Ur1 = I1 ∙ r1 = 0,3 ∙ 15 = 4,5 V.

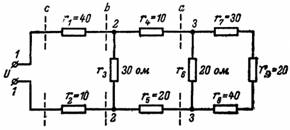
7. Şekil 2'deki devrede ortaya çıkan direnç ve akım nedir? 7 kaynak voltajı U = 220 V ise?

Pirinç. 7.

3. ve 3. düğümlerin sağında bulunan devre ile başlıyoruz. r7, r8, r9 dirençleri seri bağlı olduğundan

r (7-8-9) = r7 + r8 + r9 = 30 + 40 + 20 = 90 ohm.

Bu dirence paralel olarak bir r6 direnci bağlanır, bu nedenle düğüm 3 ve 3'te (bölüm a) ortaya çıkan direnç

ra = (r6 ∙ r (7-8-9)) / (r6 + r (7-8-9)) = (20 ∙ 90) / (20 + 90) = 1800/110 = 16,36 ohm.

Dirençler r4 ve r5, direnç ra ile seri bağlanır:

r (4-5-a) = 10 + 20 + 16,36 = 46,36 ohm.

Düğüm 2 ve 2'nin sonuç direnci (bölüm b)

rb = (r (4-5-a) ∙ r3) / (r (4-5-a) + r3) = (46,36 ∙ 30) / (46,36 + 30) = 1390,8 / 76, 36 = 18,28 ohm.

Tüm devrenin ortaya çıkan direnci r = r1 + rb + r2 = 40 + 18.28 + 10 = 68.28 ohm'dur.

Ortaya çıkan akım I = U / r = 220 / 68,28 = 3,8 A'dır.