Manyetik alan kuvveti. Mıknatıslanma kuvveti

Bir tel veya bobinin etrafında her zaman bir elektrik akımı vardır. manyetik alan… Kalıcı bir mıknatısın manyetik alanı, elektronların atomdaki yörüngelerindeki hareketinden kaynaklanır.

Bir manyetik alan, gücü ile karakterize edilir. Manyetik alanın gücü H, mekanik güce benzer. Bir vektör miktarıdır, yani büyüklüğü ve yönü vardır.

Manyetik alan yani mıknatısın etrafındaki boşluk, mıknatısın kuzey kutbundan çıkıp güney kutbuna girdiği kabul edilen manyetik çizgilerle dolu olarak gösterilebilir (Şekil 1). Manyetik çizgiye teğetler, manyetik alan şiddetinin yönünü gösterir.

Manyetik çizgilerin daha yoğun olduğu yerlerde (bir mıknatısın kutuplarında veya akım taşıyan bir bobinin içinde) manyetik alan daha güçlüdür.

Bobinin I akımı ve ω dönüş sayısı ne kadar büyük olursa, telin yakınındaki (veya bobinin içindeki) manyetik alan o kadar büyük olur.

Uzayda herhangi bir noktada H manyetik alanının gücü, ∙ ω çarpımı ne kadar büyükse ve manyetik çizginin uzunluğu o kadar kısadır:

H = (ben ∙ ω) / l.

Denklemden, manyetik alanın gücünü ölçmek için birimin metre başına amper (A / m) olduğu sonucu çıkar.

Belirli bir düzgün alandaki her manyetik çizgi için H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω eşittir (Şekil 1).

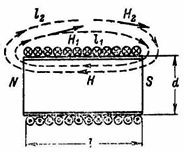
Pirinç. 1.

Manyetik devrelerdeki H ∙ l çarpımı, elektrik devrelerindeki gerilime benzer ve manyetik gerilim olarak adlandırılır ve manyetik indüksiyon hattının tüm uzunluğu boyunca alındığında mıknatıslama kuvveti (ns) olarak adlandırılır. Fm: Fm = H ∙ l = ben ∙ ω.

Mıknatıslama kuvveti Fm amper cinsinden ölçülür, ancak teknik uygulamada amper adı yerine amper-dönüş adı kullanılır, bu da Fm'nin akım ve dönüş sayısıyla orantılı olduğunu vurgular.

Uzunluğu çapından (l≫d) çok daha büyük olan, çekirdeği olmayan silindirik bir bobin için, bobin içindeki manyetik alan tek tip olarak kabul edilebilir, yani. bobinin tüm iç boşluğunda aynı manyetik alan kuvveti H ile (Şekil 1). Böyle bir bobinin dışındaki manyetik alan, içindekinden çok daha zayıf olduğundan, dış manyetik alan ihmal edilebilir ve hesaplamada n olduğu varsayılır. c bobini, bobin içindeki alan kuvvetinin bobinin uzunluğuyla çarpımına eşittir.

Telin ve akım bobininin manyetik alanının polaritesi, gimbal kuralı ile belirlenir. Eğer yalpa çemberinin ileri hareketi akımın yönü ile çakışırsa, o zaman yalpa çemberinin dönüş yönü manyetik çizgilerin yönünü gösterecektir.

Örnekleri

1. 2000 turluk bir bobinden 3 A akım geçmektedir. n nedir bobinler?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. Bobinin mıknatıslanma gücü 6000 amper dönüştür.

2. 2500 turluk bir bobin n'ye sahip olmalıdır. sayfa 10000 A. Üzerinden hangi akım geçmelidir?

ben = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.

3.Bobinden I = 2 A akımı geçiyor. n'yi sağlamak için bobinde kaç tur olması gerekir? köy 8000 A?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 dönüş.

4. 100 dönüşlü 10 cm uzunluğunda bir bobin içinde, manyetik alan kuvvetinin H = 4000 A/m olmasını sağlamak gerekir. Bobin ne kadar akım taşımalıdır?

Bobinin mıknatıslanma kuvveti Fm = H ∙ l = I ∙ ω'dir. Dolayısıyla 4000 A/m ∙ 0,1 m = ben ∙ 100; ben = 400/100 = 4 A.

5. Bobinin (solenoid) çapı D = 20 mm ve uzunluğu l = 10 cm'dir Bobin, d = 0,4 mm çapında bir bakır telden sarılır. Bobin 4,5V'ta açılırsa içindeki manyetik alan şiddeti nedir?

İzolasyon kalınlığı dikkate alınmadan dönüş sayısı ω = l∶d = 100∶0,4 = 250 dönüş.

Döngü uzunluğu π ∙ d = 3,14 ∙ 0,02 m = 0,0628 m.

Bobin uzunluğu l1 = 250 ∙ 0,0628 m = 15,7 m.

Bobinin aktif direnci r = ρ ∙ l1 / S = 0,0175 ∙ (4 ∙ 15,7) / (3,14 ∙ 0,16) = 2,2 Ohm.

Akım ben = U / r = 4,5 / 2,2 = 2,045 A ≈2 A.

Bobin içindeki manyetik alanın gücü H = (I ∙ ω) / l = (2 ∙ 250) / 0,1 = 5000 A / m.

6. İçinden I = 100 A akımın aktığı düz telden 1, 2, 5 cm mesafedeki manyetik alanın gücünü belirleyin.

H ∙ l = I ∙ ω formülünü kullanalım.

Düz bir tel için ω = 1 ve l = 2 ∙ π ∙ r,

bu nedenle H = ben / (2 ∙ π ∙ r).

H1 = 100 / (2 ∙ 3,14 ∙ 0,01) = 1590 A / m; H2 = 795 A/dak; H3 = 318 A/dak.