Kayıplar ve voltaj düşüşleri - farklar nelerdir

Sıradan insan hayatında, "kayıp" ve "düşme" kelimeleri, belirli başarıların azaldığı gerçeğini belirtmek için kullanılır, ancak bunlar farklı bir değeri ifade eder.

Bu durumda, "kayıplar", bir parçanın kaybı, hasar, daha önce ulaşılan seviyenin boyutunun küçülmesi anlamına gelir. Kayıplar istenmez, ancak onları tolere edebilirsiniz.

"Düşme" kelimesi, hakların tamamen yoksun bırakılmasıyla ilişkili daha ciddi bir zarar olarak anlaşılmaktadır. Bu nedenle, zaman içinde ara sıra meydana gelen kayıplar (örneğin bir portföy) bile bir düşüşe (örneğin, maddi yaşam seviyesi) yol açabilir.

Bu bağlamda, elektrik şebekesinin voltajı ile ilgili olarak bu soruyu ele alacağız.

Kayıplar ve voltaj düşüşleri nasıl oluşur?

Elektrik, bir trafo merkezinden diğerine havai hatlarla uzun mesafeler boyunca taşınır.

Havai hatlar, izin verilen gücü iletmek için tasarlanmıştır ve belirli bir malzeme ve kesitteki metal tellerden yapılmıştır. Direnç değeri R olan dirençli bir yük ve X reaktif yükü oluştururlar.

Alıcı tarafta duruyor trafoelektrik dönüşümü.Bobinleri, aktif ve belirgin bir endüktif direnç XL'ye sahiptir. Transformatörün ikincil tarafı voltajı düşürür ve yükü Z değeri ile ifade edilen ve doğası gereği aktif, kapasitif ve endüktif olan tüketicilere iletir. Bu aynı zamanda ağın elektriksel parametrelerini de etkiler.

Enerji nakil trafo merkezine en yakın olan havai hat desteğinin tellerine uygulanan voltaj, devrenin her fazdaki reaktif ve aktif direncini aşar ve içinde vektörü vektöründen sapan bir akım oluşturur. φ açısı kadar uygulanan gerilim.

Simetrik bir yük modu için hat boyunca voltaj dağılımının ve akım akışının doğası fotoğrafta gösterilmiştir.

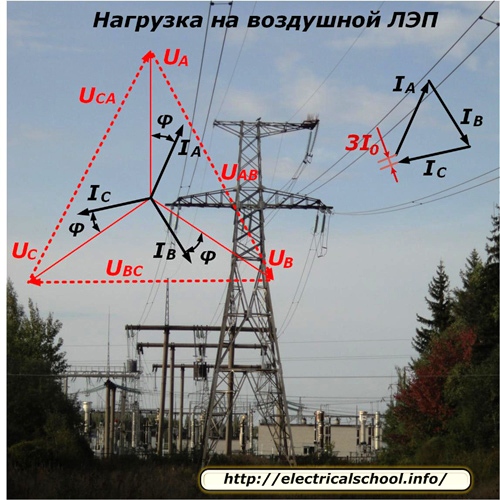
Hattın her fazı, aynı zamanda rastgele bağlantısı kesilen veya işe bağlanan farklı sayıda tüketiciyi beslediğinden, faz yükünü mükemmel bir şekilde dengelemek teknik olarak çok zordur. Faz akımlarının vektörel toplamı ile belirlenen ve 3I0 olarak yazılan bir dengesizlik içinde her zaman vardır. Çoğu hesaplamada basitçe göz ardı edilir.

Verici trafo merkezi tarafından tüketilen enerji kısmen hattın direncini aşmak için harcanır ve çok az değişiklikle alıcı tarafa ulaşır. Bu fraksiyon, vektörü genlikte hafifçe azalan ve her fazda bir açıyla kaydırılan kayıp ve voltaj düşüşü ile karakterize edilir.

Kayıplar ve voltaj düşüşü nasıl hesaplanır?

Elektriğin iletimi sırasında meydana gelen süreçleri anlamak için vektör formu, ana özellikleri temsil etmesi açısından uygundur. Çeşitli matematiksel hesaplama yöntemleri de bu yönteme dayanmaktadır.

Hesaplamaları basitleştirmek için üç fazlı sistem üç tek fazlı eşdeğer devre ile temsil edilir. Bu yöntem simetrik bir yükle iyi çalışır ve kırıldığında süreçleri analiz etmenizi sağlar.

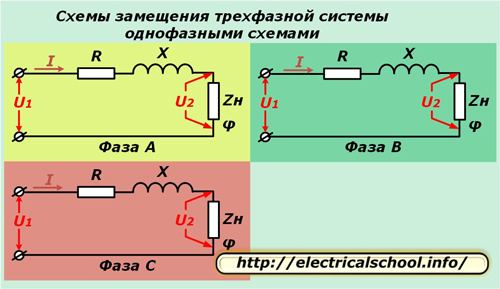
Yukarıdaki şemalarda, hattın her bir iletkeninin aktif R ve reaktansı X, φ açısı ile karakterize edilen kompleks yük direnci Zn ile seri olarak bağlanmıştır.

Ayrıca bir fazda gerilim kaybı ve gerilim düşümü hesabı yapılır. Bunu yapmak için verileri belirtmeniz gerekir. Bu amaçla, izin verilen yükün önceden belirlenmesi gereken enerji alan bir trafo merkezi seçilir.

Herhangi bir yüksek voltaj sisteminin voltaj değeri referans kitaplarında zaten belirtilmiştir ve tellerin dirençleri uzunlukları, kesitleri, malzemeleri ve ağın konfigürasyonu ile belirlenir. Devredeki maksimum akım, tellerin özellikleri tarafından belirlenir ve sınırlandırılır.

Bu nedenle, hesaplamalara başlamak için elimizde şunlar var: U2, R, X, Z, I, φ.

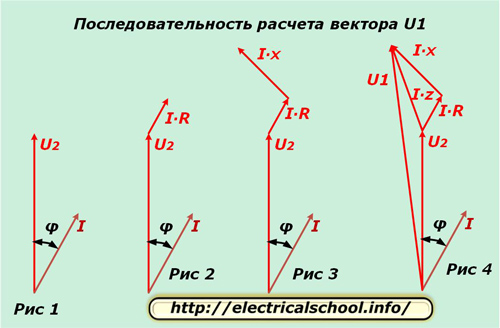
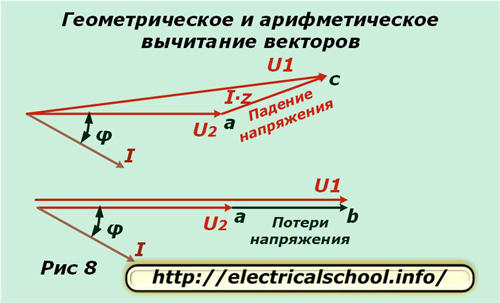
Örneğin «A» gibi bir fazı alıyoruz ve onun için karmaşık düzlemde U2 ve I vektörlerini Şekil 1'de gösterildiği gibi bir φ açısı ile yer değiştirmiş olarak ayırıyoruz. İletkenin aktif direncindeki potansiyel fark, yönde çakışıyor akım ile ve büyüklük olarak I ∙ R ifadesinden belirlenir. Bu vektörü U2'nin sonundan erteleriz (Şekil 2).

İletkenin reaktansındaki potansiyel fark, akımın yönünden φ1 açısı kadar farklılık gösterir ve I ∙ X ürününden hesaplanır. I ∙ R vektöründen erteliyoruz (Şekil 3).

Hatırlatmalar: Karmaşık düzlemde vektörlerin pozitif dönüş yönü için saat yönünün tersine hareket alınır. Endüktif yükten akan akım, uygulanan voltajın bir açı kadar gerisindedir.

Şekil 4, I ∙ Z toplam kablo direnci ve U1 devresinin girişindeki voltaj üzerindeki potansiyel fark vektörlerinin grafiğini göstermektedir.

Artık giriş vektörlerini eşdeğer devreye ve yüke göre karşılaştırabilirsiniz. Bunu yapmak için, ortaya çıkan diyagramı yatay olarak yerleştirin (Şekil 5) ve U1 modülünün yarıçapı ile baştan U2 vektörünün yönüyle kesişene kadar bir yay çizin (Şekil 6).

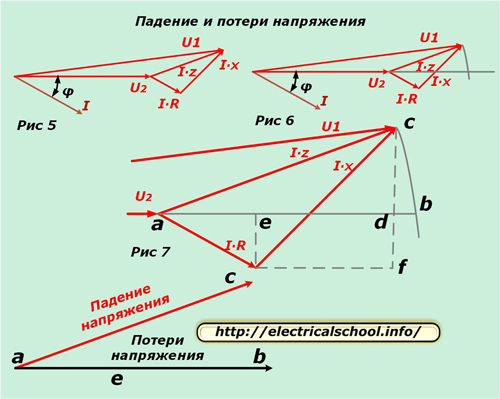
Şekil 7, daha fazla netlik için üçgenin büyütülmüş halini ve harflerle karakteristik kesişme noktalarını gösteren yardımcı çizgilerin çizimini göstermektedir.

Resmin alt kısmında, ortaya çıkan vektör ac'nin gerilim düşüşü ve ab'nin kayıp olarak adlandırıldığı gösterilmektedir. Boyut ve yön bakımından farklılık gösterirler. Orijinal ölçeğe dönersek, ac'nin vektörlerin (U2'den U1'den) geometrik olarak çıkarılması sonucunda elde edildiğini ve ab'nin aritmetik olduğunu göreceğiz. Bu işlem aşağıdaki resimde gösterilmektedir (Şekil 8).

Gerilim kayıplarını hesaplamak için formüllerin türetilmesi

Şimdi Şekil 7'ye geri dönelim ve bd segmentinin çok küçük olduğuna dikkat edelim. Bu nedenle hesaplamalarda ihmal edilir ve ad segment uzunluğundan gerilim kaybı hesaplanır. ae ve ed olmak üzere iki doğru parçasından oluşur.

ae = I ∙ R ∙ cosφ ve ed = I ∙ x ∙ sinφ olduğundan, bir faz için voltaj kaybı aşağıdaki formülle hesaplanabilir:

∆Uf = ben ∙ R ∙ cosφ + ben ∙ x ∙ sinφ

Yükün tüm fazlarda simetrik olduğunu varsayarsak (koşullu olarak 3I0'u ihmal ederek), hattaki gerilim kaybını hesaplamak için matematiksel yöntemler kullanabiliriz.

∆Ul = √3I ∙ (R ∙ cosφ + x ∙ sinφ)

Bu formülün sağ tarafı, Un şebeke gerilimi ile çarpılır ve bölünürse, o zaman gerçekleştirmemizi sağlayan bir formül elde ederiz. pGüç kaynağı üzerinden gerilim kayıplarının hesaplanması.

∆Ul = (P ∙ r + Q ∙ x) / Un

Aktif P ve reaktif Q güç değerleri hat sayaç okumalarından alınabilir.

Bu nedenle, bir elektrik devresindeki voltaj kaybı şunlara bağlıdır:

• devrenin aktif ve reaktansı;

• uygulanan gücün bileşenleri;

• uygulanan voltajın büyüklüğü.

Gerilim düşüşünün enine bileşenini hesaplamak için formüllerin türetilmesi

Şekil 7'ye geri dönelim. Ac vektörünün değeri, bir acd dik üçgeninin hipotenüsüyle temsil edilebilir. Reklam ayağını zaten hesapladık. Enine bileşen cd'yi belirleyelim.

Şekil cd = cf-df olduğunu göstermektedir.

df = ce = ben ∙ R ∙ sin φ.

cf = ben ∙ x ∙ çünkü φ.

cd = ben ∙ x ∙ cosφ-I ∙ R ∙ sinφ.

Elde edilen modelleri kullanarak küçük matematiksel dönüşümler gerçekleştiriyor ve gerilim düşüşünün enine bileşenini elde ediyoruz.

δU = √3I ∙ (x ∙ cosφ-r ∙ sinφ) = (P ∙ x-Q ∙ r) / Un.

Güç hattının başlangıcındaki U1 voltajını hesaplamak için formülün belirlenmesi

U2 hattının sonundaki voltajın değerini, kaybı ∆Ul ve düşüşün enine bileşenini δU bilerek, Pisagor teoremi ile U1 vektörünün değerini hesaplayabiliriz. Genişletilmiş formda, aşağıdaki forma sahiptir.

U1 = √ [(U2 + (Pr + Qx) / Un)2+ ((Px-Qr) / Un)2].

Pratik kullanım

Gerilim kayıplarının hesaplanması, ağ konfigürasyonunun ve onu oluşturan elemanların optimum seçimi için bir elektrik devresi projesi oluşturma aşamasında mühendisler tarafından gerçekleştirilir.

Elektrik tesisatlarının işletilmesi sırasında gerekirse hatların uçlarındaki gerilim vektörlerinin eş zamanlı ölçümleri periyodik olarak yapılabilir ve basit hesaplamalar yöntemiyle elde edilen sonuçlar karşılaştırılabilir.Bu yöntem artan cihazlar için uygundur. yüksek iş doğruluğu ihtiyacı nedeniyle gereksinimler.

Sekonder devrelerde gerilim kayıpları

Bir örnek, bazen birkaç yüz metre uzunluğa ulaşan ve kesiti artırılmış özel bir güç kablosuyla iletilen gerilim trafolarını ölçen sekonder devrelerdir.

Böyle bir kablonun elektriksel özellikleri, voltaj iletiminin kalitesi için artan gereksinimlere tabidir.

Elektrikli ekipmanın modern koruması, yüksek metrolojik göstergelere ve 0,5 veya hatta 0,2 doğruluk sınıfına sahip ölçüm sistemlerinin çalışmasını gerektirir. Bu nedenle bunlara uygulanan gerilimdeki kayıplar izlenmeli ve dikkate alınmalıdır. Aksi takdirde, ekipmanın çalışmasına getirdikleri hata, tüm çalışma özelliklerini önemli ölçüde etkileyebilir.

Uzun kablo hatlarında gerilim kayıpları

Uzun kablonun tasarımının özelliği, iletken damarların oldukça yakın düzenlenmesi ve aralarında ince bir yalıtım tabakası olması nedeniyle kapasitif bir dirence sahip olmasıdır. Kablodan geçen akım vektörünü daha da saptırır ve büyüklüğünü değiştirir.

I ∙ z değerini değiştirmek için yapılan hesaplamada gerilim düşüşünün kapasitif direnç üzerindeki etkisi dikkate alınmalıdır. Aksi takdirde, yukarıda açıklanan teknoloji değişmez.

Makale, havai elektrik hatları ve kablolardaki kayıplara ve voltaj düşüşlerine örnekler sağlar. Bununla birlikte, elektrik motorları, transformatörler, indüktörler, kapasitör bankları ve diğer cihazlar da dahil olmak üzere tüm elektrik tüketicilerinde bulunurlar.

Her tip elektrikli ekipman için voltaj kayıplarının miktarı, çalışma koşulları açısından yasal olarak düzenlenmiştir ve bunların tüm elektrik devrelerinde belirlenme prensibi aynıdır.