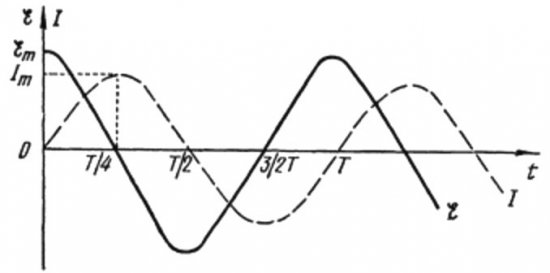
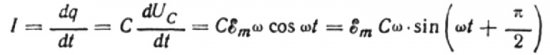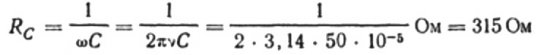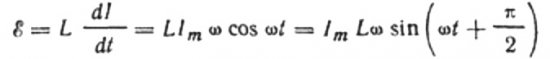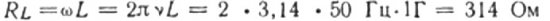Alternatif akım devresinde kapasitif ve endüktif direnç

Bir DC devresine bir kapasitör eklersek, sonsuz dirence sahip olduğunu buluruz çünkü bir dielektrik tanımı gereği bir doğru elektrik akımı iletmediği için doğru akım plakalar arasındaki dielektrikten geçemez.

Bir kondansatör DC devresini keser. Ancak, aynı kapasitör şimdi alternatif akım devresine dahil edilirse, kapasitörünün tamamen kırılmadığı, basitçe değiştiği ve şarj olduğu, yani elektrik yükünün hareket ettiği ve dış devredeki akımın olduğu ortaya çıktı. bakımlı

Bu durumda Maxwell'in teorisine dayanarak, kondansatör içindeki alternatif iletim akımının sadece bu durumda önyargı akımı tarafından hala kapalı olduğunu söyleyebiliriz. Bu, AC devresindeki kapasitörün bir tür sonlu değer direnci gibi davrandığı anlamına gelir. Bu dirence denir kapasitif.

Uygulama, bir iletkenden akan alternatif akımın miktarının, o iletkenin şekline ve etrafındaki ortamın manyetik özelliklerine bağlı olduğunu uzun zamandır göstermiştir.Düz bir tel ile akım en büyük olacaktır ve aynı tel çok sayıda sarımı olan bir bobine sarılırsa akım daha az olacaktır.

Ve aynı bobine bir ferromanyetik çekirdek sokulursa, akım daha da azalacaktır. Bu nedenle tel, yalnızca omik (aktif) bir dirençle değil, aynı zamanda telin endüktansına bağlı olarak ek bir dirençle de alternatif akım sağlar.Bu direnç denir. endüktif.

Fiziksel anlamı, belirli bir endüktansa sahip bir iletkende değişen bir akımın, bu iletkende akımdaki değişiklikleri önleme, yani akımı azaltma eğiliminde olan bir kendi kendine endüksiyon EMF'sini başlatmasıdır. Bu, telin direncini artırmaya eşdeğerdir.

AC devresindeki kapasitans

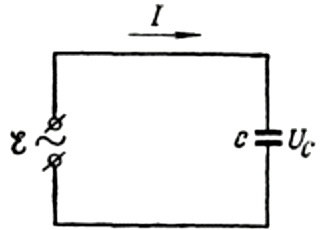
Öncelikle kapasitif dirençten daha detaylı bahsedelim. Bir sinüzoidal alternatif akım kaynağına C kapasitans kapasitörünün bağlandığını varsayalım, daha sonra bu kaynağın EMF'si aşağıdaki formülle açıklanacaktır:

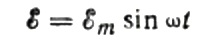
Genellikle çok küçük olduğundan ve gerekirse ayrı olarak değerlendirilebileceğinden, bağlantı kablolarındaki voltaj düşüşünü göz ardı edeceğiz. Şimdi kondansatör plakalarındaki voltajın AC kaynak voltajına eşit olduğunu varsayalım. Daha sonra:

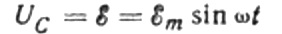
Herhangi bir anda, bir kondansatörün yükü kapasitansına ve plakaları arasındaki gerilime bağlıdır. Daha sonra, yukarıda bahsedilen bilinen kaynak göz önüne alındığında, kaynak voltajı ile kapasitör plakalarındaki yükü bulmak için bir ifade elde ederiz:

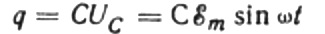
Sonsuz küçük bir dt süresi için kondansatör üzerindeki yükün dq kadar değişmesine izin verin, daha sonra tellerden kaynaktan kondansatöre şuna eşit bir I akımı akacaktır:

Mevcut genliğin değeri şuna eşit olacaktır:

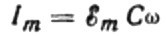
O zaman akım için son ifade şöyle olacaktır:

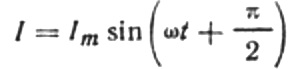
Mevcut genlik formülünü aşağıdaki gibi yeniden yazalım:

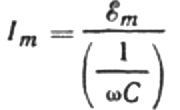
Bu oran, açısal frekans ve kapasitans çarpımının direncin rolünü oynadığı Ohm yasasıdır ve aslında sinüzoidal bir alternatif akım devresindeki bir kapasitörün kapasitansını bulmak için bir ifadedir:

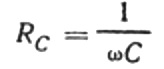
Bu, kapasitif direncin, akımın açısal frekansı ve kapasitörün kapasitansı ile ters orantılı olduğu anlamına gelir. Bu bağımlılığın fiziksel anlamını anlamak kolaydır.

AC devresindeki kapasitörün kapasitansı ne kadar büyükse ve bu devredeki akımın yönü ne kadar sık ​​değişirse, sonuçta kapasitörü AC kaynağına bağlayan tellerin kesitinden birim zamanda daha fazla toplam yük geçer. Bu, akımın kapasitans ve açısal frekansın ürünü ile orantılı olduğu anlamına gelir.

Örneğin, 50 Hz frekanslı sinüzoidal bir alternatif akım devresi için elektrik kapasitesi 10 mikrofarad olan bir kapasitörün kapasitansını hesaplayalım:

Frekans 5000 Hz olsaydı, aynı kapasitör yaklaşık 3 ohm'luk bir direnç gösterirdi.

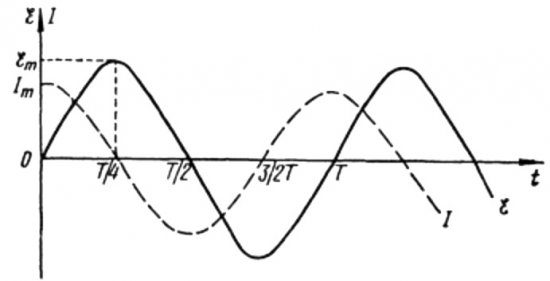
Yukarıdaki formüllerden, kapasitörlü bir AC devresindeki akım ve voltajın her zaman farklı fazlarda değiştiği açıktır. Akım fazı gerilim fazından pi / 2 (90 derece) öndedir. Bu, zaman içindeki maksimum akımın her zaman maksimum voltajdan çeyrek periyot önce var olduğu anlamına gelir. Böylece, kapasitif direnç boyunca akım, gerilimden zamanın dörtte biri veya fazda 90 derece öndedir.

Bu fenomenin fiziksel anlamını açıklayalım.İlk anda, kapasitör tamamen boşalır, bu nedenle ona uygulanan en ufak bir voltaj, kapasitörün plakalarındaki yükleri hareket ettirerek bir akım oluşturur.

Kondansatör şarj olurken, plakalarındaki voltaj artar, bu da daha fazla yük akışını engeller, bu nedenle plakalara uygulanan voltajdaki daha fazla artışa rağmen devredeki akım azalır.

Bu, ilk anda akım maksimum ise, gerilim çeyrek periyottan sonra maksimuma ulaştığında akımın tamamen duracağı anlamına gelir.

Periyodun başında akım maksimum ve voltaj minimumdur ve yükselmeye başlar ancak periyodun dörtte birinden sonra voltaj maksimuma ulaşır ancak bu zamana kadar akım çoktan sıfıra düşmüştür. Böylece gerilimin gerilimden periyodun dörtte biri kadar önde olduğu ortaya çıkar.

AC endüktif direnç

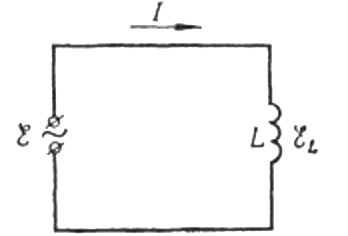
Şimdi endüktif dirence geri dönelim. Alternatif bir sinüzoidal akımın bir endüktans bobininden geçtiğini varsayalım. Şu şekilde ifade edilebilir:

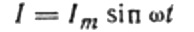
Akım, bobine uygulanan alternatif voltajdan kaynaklanır. Bu, bobinde aşağıdaki gibi ifade edilen bir kendi kendine indüksiyon EMF'sinin görüneceği anlamına gelir:

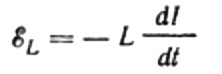
Yine, EMF kaynağını bobine bağlayan teller üzerindeki voltaj düşüşünü ihmal ediyoruz. Ohmik dirençleri çok düşüktür.

Herhangi bir anda bobine uygulanan alternatif voltajın, büyüklük olarak kendisine eşit ancak zıt yönde ortaya çıkan kendi kendine endüksiyon EMF'si ile tamamen dengelenmesine izin verin:

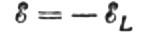
O zaman şunu yazmaya hakkımız var:

Bobine uygulanan voltajın genliği:

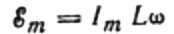
alırız:

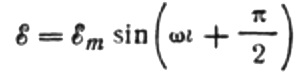
Maksimum akımı şu şekilde ifade edelim:

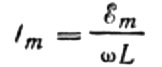
Bu ifade aslında Ohm yasasıdır. Endüktansın ve açısal frekansın ürününe eşit bir miktar burada direnç rolünü oynar ve indüktörün endüktif direncinden başka bir şey değildir:

Dolayısıyla, endüktif direnç, bobinin endüktansı ve bu bobinden geçen alternatif akımın açısal frekansı ile orantılıdır.

Bunun nedeni, endüktif direncin, kendi kendine endüksiyon EMF'nin kaynak voltajı üzerindeki etkisinden kaynaklanmasıdır, - kendi kendine endüksiyon EMF, akımı azaltma eğilimindedir ve bu nedenle devrede direnç getirir. Bilindiği gibi, kendi kendine endüksiyon emf'sinin büyüklüğü, bobinin endüktansı ve içinden geçen akımın değişim hızı ile orantılıdır.

Örneğin, akım frekansı 50 Hz olan bir devreye dahil olan 1 H endüktanslı bir bobinin endüktif direncini hesaplayalım:

Topun frekansı 5000 Hz olsaydı, aynı bobinin direnci yaklaşık 31.400 ohm olurdu.Bobin telinin omik direncinin genellikle birkaç ohm olduğunu hatırlayın.

Yukarıdaki formüllerden, bobinden geçen akım ve içindeki voltajdaki değişikliklerin farklı fazlarda meydana geldiği ve akımın fazının her zaman pi / 2'deki voltajın fazından daha az olduğu açıktır. maksimum akım, maksimum gerilimin başlangıcından çeyrek periyot sonra gerçekleşir.

Endüktif dirençte, akımın değişmesini (hem artmasını hem de azalmasını) önleyen kendinden indüklenmiş EMF'nin frenleme etkisi nedeniyle akım gerilimden 90 derece geridedir, bu nedenle bobin ile devrede daha sonra maksimum akım gözlenir. maksimum voltajdan daha fazla.

Bobin ve kapasitör birleşik eylem

Alternatif akım devresine seri olarak kondansatörlü bir bobin bağlarsanız, bobin voltajı kondansatör voltajını zaman içinde yarım periyot, yani fazda 180 derece ilerletecektir.

Kapasitif ve endüktif direnç denir tepkenler… Aktif dirençte olduğu gibi reaktif dirençte enerji harcanmaz. Kondansatörde depolanan enerji, kondansatördeki elektrik alan kaybolduğunda periyodik olarak kaynağa geri döner.

Bobinde de durum aynıdır: Bobinin manyetik alanı akım tarafından yaratıldığı için, periyodun bir çeyreğinde içindeki enerji birikir ve sonraki çeyrekte kaynağa geri döner. Bu yazıda, bu yönetmeliklere sıkı sıkıya uyulan sinüzoidal alternatif akımdan bahsettik.

AC sinüzoidal devrelerde, özlü indüktörler denir boğucugeleneksel olarak akım sınırlaması için kullanılırlar. Reostalara göre avantajları, enerjinin ısı olarak büyük miktarlarda dağılmamasıdır.