endüktans nasıl hesaplanır
Tıpkı mekanikte kütleye sahip bir cismin uzayda ivmeye direnerek atalete direnmesi gibi, endüktans da bir iletkendeki akımın değişmesini engelleyerek kendinden endüksiyonlu EMF'yi gösterir. Bu, hem akımın azalmasına, onu korumaya çalışmasına hem de akımın artmasına, onu azaltmaya çalışmasına karşı çıkan kendi kendine indüksiyonun EMF'sidir.
Gerçek şu ki, devredeki akımı değiştirme (arttırma veya azaltma) sürecinde, bu akımın yarattığı manyetik akı da değişir ve bu, esas olarak bu devre tarafından sınırlanan alanda lokalize olur. Ve manyetik akı arttıkça veya azaldıkça, hepsi aynı devrede (Lenz kuralına göre - buna neden olan nedene, yani başlangıçta bahsedilen akıma karşı) kendi kendine indüksiyonlu bir EMF'yi indükler. Buradaki endüktans L, akım I ile toplam manyetik akı Φ arasındaki orantı faktörü olarak adlandırılır, bu akım şu şekilde üretilir:
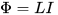
Böylece, devrenin endüktansı ne kadar yüksek olursa, ortaya çıkan manyetik alandan o kadar güçlü olur, akımın değişmesini engeller (bunu oluşturan alandır) ve bu nedenle akımın daha büyük endüktans yoluyla değişmesi daha uzun sürer, aynı uygulanan voltaj ile. Aşağıdaki ifade de doğrudur: endüktans ne kadar yüksek olursa, içinden geçen manyetik akı değiştiğinde devre boyunca voltaj o kadar yüksek olacaktır.

Belirli bir bölgedeki manyetik akıyı sabit bir oranda değiştirdiğimizi varsayalım, sonra bu bölgeyi farklı devrelerle kaplayarak endüktansı büyük olan devrede daha fazla gerilim elde edeceğiz (trafo, Rumkorf bobini vb. bu prensiple çalışır).
Ancak döngü endüktansı nasıl hesaplanır? Akım ve manyetik akı arasındaki orantı faktörü nasıl bulunur? Hatırlanması gereken ilk şey, endüktansın henry (H) cinsinden değiştiğidir. Endüktansı 1 henry olan bir devrenin uçlarında, içindeki akım saniyede bir amper değişirse, 1 voltluk bir voltaj görünecektir.
Endüktansın büyüklüğü iki parametreye bağlıdır: devrenin geometrik boyutlarına (uzunluk, genişlik, dönüş sayısı vb.) ve ortamın manyetik özelliklerine (örneğin, içinde bir ferrit çekirdek varsa) bağlıdır. bobin, endüktansı, içinde çekirdek olmadığı duruma göre daha büyük olacaktır).
Üretilen endüktansı hesaplamak için, bobinin kendisinin nasıl bir şekle sahip olacağını ve içindeki ortamın hangi manyetik geçirgenliğe sahip olacağını bilmek gerekir (ortamın göreli manyetik geçirgenliği, bir vakumun manyetik geçirgenliği ile manyetik arasındaki orantı faktörüdür. Belirli bir ortamın geçirgenliği.Tabii ki, farklı malzemeler için farklıdır) …
En yaygın bobin biçimlerinin (silindirik solenoid, toroid ve uzun tel) endüktansını hesaplamak için formüllere bakalım.
İşte endüktansı hesaplamak için formül solenoid - uzunluğu çaptan çok daha büyük olan bobinler:
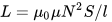
Gördüğünüz gibi, N dönüş sayısını, sargının uzunluğunu l ve bobinin S kesit alanını bilerek, bobinin çekirdeksiz veya çekirdekli yaklaşık endüktansını bulurken, manyetik vakumun geçirgenliği sabit bir değerdir:
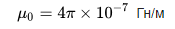
Bir toroidal bobinin endüktansı, burada h, toroidin yüksekliğidir, r, toroidin iç çapıdır, R, toroidin dış çapıdır:
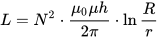
İnce bir telin endüktansı (kesitin yarıçapı, uzunluğundan çok daha küçüktür), burada l, telin uzunluğu ve r, kesitinin yarıçapıdır. i ve e endeksli Mu, iç (iç, iletken malzemeler) ve dış (dış, iletken dışındaki malzemeler) ortamların göreli manyetik geçirgenlikleri:
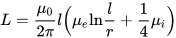
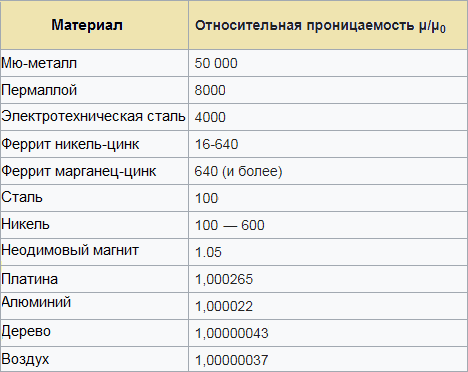
Bağıl geçirgenlikler tablosu, çekirdek olarak belirli bir manyetik malzeme kullanan bir devreden (tel, bobin) ne kadar endüktans bekleyebileceğinizi tahmin etmenize yardımcı olacaktır: