iç direnç nedir

Jeneratör, galvanik hücre veya pil gibi bir akım kaynağı ve R direncine sahip bir direnç içeren basit bir elektriksel kapalı devre olduğunu varsayalım. Devredeki akım hiçbir yerde kesilmediği için kaynağın içinde de akar.

Böyle bir durumda her kaynağın akımın akmasını engelleyen bir iç direnci olduğunu söyleyebiliriz. Bu iç direnç, akım kaynağını karakterize eder ve r harfi ile gösterilir. İçin galvanic hücre veya pil, iç direnç, bir jeneratör için elektrolit çözeltisinin ve elektrotların direncidir - stator sargılarının direnci, vb.

Bu nedenle, bir akım kaynağı hem EMF'nin büyüklüğü hem de kendi iç direncinin değeri r ile karakterize edilir - her iki özellik de kaynağın kalitesini gösterir.

Örneğin, yüksek voltajlı elektrostatik jeneratörler (Van de Graaf jeneratörü veya Wimshurst jeneratörü gibi), iç dirençleri yüzlerce megohm olarak ölçülürken milyonlarca voltla ölçülen devasa bir EMF'ye sahiptir, bu nedenle elde etmek için uygun değildirler. yüksek akımlar

Aksine, galvanik piller (bir pil gibi), iç dirençleri kesirler mertebesinde veya en fazla on ohm olmasına rağmen, 1 volt mertebesinde bir EMF'ye sahiptir ve bu nedenle birim akımlar ve onlarca amper elde edilebilir. galvanik hücrelerden.

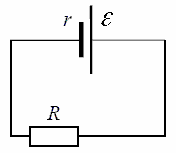
Bu şema, bağlı bir yükle gerçek bir kaynağı göstermektedir. Burada tanımlanmışlar EMF kaynağı, iç direncinin yanı sıra yük direnci. Buna göre Kapalı devre için Ohm yasası, bu devredeki akım şuna eşit olacaktır:

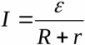
Devrenin dış bölümü homojen olduğundan, Ohm yasasından yük üzerindeki voltaj bulunabilir:

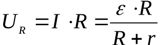
Yükün direncini birinci denklemden ifade ederek ve değerini ikinci denklemde değiştirerek, yükteki voltajın kapalı bir devredeki akıma bağımlılığını elde ederiz:

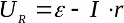
Kapalı bir döngüde EMF, dış devre elemanlarındaki ve kaynağın kendisinin iç direncindeki voltaj düşüşünün toplamına eşittir. Yük voltajının yük akımına bağımlılığı ideal olarak doğrusaldır.

Grafik bunu gösterir, ancak gerçek bir direnç için deneysel veriler (grafiğe yakın kesişir) her zaman idealden farklıdır:

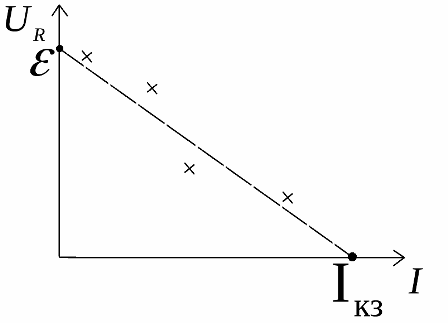
Deneyler ve mantık, sıfır yük akımında harici devre voltajının kaynak emf'ye eşit olduğunu ve sıfır yük voltajında ​​devre akımının kısa devre akımı... Gerçek devrelerin bu özelliği, gerçek kaynakların EMF'sini ve iç direncini deneysel olarak bulmaya yardımcı olur.

İç direncin deneysel tespiti

Bu özellikleri deneysel olarak belirlemek için, yükteki voltajın akımın büyüklüğüne bağımlılığının bir grafiği oluşturulur ve ardından eksenlerle kesişme noktasına ekstrapolasyon yapılır.

Grafiğin voltaj omurgası ile kesişme noktasında kaynak emf'nin değeri ve akım ekseni ile kesişme noktasında kısa devre akımının değeri bulunur. Sonuç olarak, iç direnç aşağıdaki formülle bulunur:

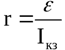
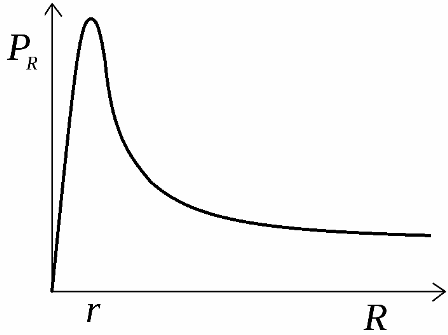
Kaynak tarafından geliştirilen faydalı güç, yük boyunca dağıtılır. Bu gücün yük direncine bağımlılığının grafiği şekilde gösterilmiştir. Bu eğri, koordinat eksenlerinin sıfır noktasında kesişmesinden başlar, sonra maksimum güç değerine yükselir, sonra sonsuza eşit bir yük direnci ile sıfıra düşer.

Belirli bir kaynakla teorik maksimum gücün geliştirileceği maksimum yük direncini bulmak için, güç formülünün R'ye göre türevi alınır ve sıfıra ayarlanır. Maksimum güç, harici devre direnci dahili kaynak direncine eşit olduğunda geliştirilecektir:

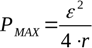
R = r'deki maksimum güç için bu hüküm, yükte salınan gücü yük direncinin değerine karşı çizerek kaynağın iç direncini deneysel olarak bulmanızı sağlar.Maksimum güç sağlayan teorik yerine gerçek bir yük direnci bulmak, güç kaynağının gerçek iç direncini belirler.

Akım kaynağının verimliliği, yüke dağıtılan maksimum gücün halihazırda geliştirilmekte olan toplam güce oranını gösterir.

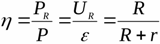
Kaynak, yükte belirli bir kaynak için mümkün olan maksimum gücü elde edecek kadar güç geliştirirse, kaynağın veriminin %50'ye eşit olacağı açıktır.