akımların rezonansı

Alternatif akım devresinde bir kondansatör ve bir indüktörün paralel bağlantısı

Zincirdeki olayları göz önünde bulundurun alternatif akımparalel bağlı bir jeneratör, kondansatör ve indüktör içerir. Devrenin aktif direncinin olmadığını varsayalım.

Açıkçası, böyle bir devrede hem bobinin hem de kondansatörün voltajı herhangi bir zamanda jeneratör tarafından geliştirilen voltaja eşittir.

Bir devredeki toplam akım, kollarındaki akımlardan oluşur. Endüktif daldaki akım, fazdaki voltajın periyodun dörtte biri kadar gerisinde kalır ve kapasitif koldaki akım, periyodun aynı çeyreği kadar öndedir. Bu nedenle, herhangi bir anda kollardaki akımlar birbirlerine göre yarım periyot faz kaymalı, yani antifazdadırlar. Böylece her an dallardaki akımlar birbirine doğru yönelir ve devrenin dallanmamış kısmındaki toplam akım bunların farkına eşittir.

Bu bize I = IL -integral devresi eşitliğini yazma hakkını verir.

Neredeyim- devredeki toplam akımın etkin değeri, I L ve entegre devre — dallardaki akımların etkin değerleri.

Dallardaki akımın etkin değerlerini belirlemek için Ohm yasasını kullanarak şunu elde ederiz:

Il = U / XL ve Az° C = U / XC

Devreye endüktif direnç hakimse, yani. XL Daha Fazla ▼ XC, bobindeki akım kondansatördeki akımdan daha azdır; bu nedenle, devrenin dallanmamış bölümündeki akım doğası gereği kapasitiftir ve jeneratör için devre bir bütün olarak kapasitif olacaktır. Tersine, XC XL'den büyük olduğunda, kondansatördeki akım bobindeki akımdan daha azdır; bu nedenle devrenin dallanmamış bölümündeki akım endüktiftir ve jeneratör için devre bir bütün olarak endüktif olacaktır.

Unutulmamalıdır ki her iki durumda da yük reaktiftir, yani; devre, jeneratörün gücünü tüketmez.

akımların rezonansı

Şimdi paralel bağlanan kapasitör ve bobinin reaktanslarında eşit olduğu durumu ele alalım, yani. XIL = X°C.

Daha önce olduğu gibi, bobin ve kondansatörün aktif direncinin olmadığını varsayarsak, reaksiyonları eşitse (YL = Y° C), devrenin dallanmamış kısmındaki toplam akım sıfır olurken, dallardaki akım eşittir. akımlar en büyük büyüklükle akacaktır. Bu durumda, devrede rezonans akımları olgusu meydana gelir.

Akım rezonansında her daldaki akımların IL = U / XL ve Аz° С = U / XC oranları ile belirlenen efektif değerleri birbirine eşit olacağından XL = XC olacaktır.

Vardığımız sonuç ilk bakışta oldukça garip gelebilir. Aslında, jeneratör iki dirençle yüklenir ve devrenin dallanmamış kısmında akım yoktur, eşit ve dahası en büyük akımlar dirençlerin kendisinde akar.

Bu, bobinin manyetik alanının davranışı ile açıklanır ve bir kondansatörün elektrik alanı… Akımların rezonansında, olduğu gibi voltaj rezonansı, bobinin alanı ile kondansatörün alanı arasında bir enerji dalgalanması vardır. Jeneratör, enerjiyi devreye ilettikten sonra izole edilmiş gibi görünür. Tamamen kapatılabilir ve devrenin kollara ayrılmış kısmındaki akım, devrenin başlangıçta depoladığı enerji ile bir jeneratör olmadan korunur. Ayrıca, devre terminalleri arasındaki voltaj, jeneratör tarafından geliştirilenle tamamen aynı kalacaktır.

Böylece, indüktör ve kondansatör paralel bağlandığında, yukarıda açıklanandan farklı olarak, yalnızca salınımları oluşturan jeneratörün devreye doğrudan bağlanmaması ve devrenin kapalı olması nedeniyle bir osilatör devresi elde ettik. 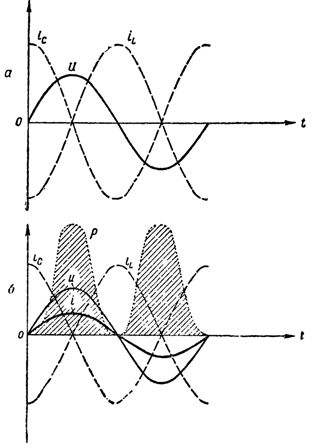Akım rezonansında devredeki akım, voltaj ve güç grafikleri: a — aktif direnç sıfıra eşittir, devre enerji tüketmez; b — devrenin aktif bir direnci var, devrenin dallanmamış kısmında bir akım belirdi, devre enerji tüketiyor

Akım rezonansının meydana geldiği L, C ve e, voltaj rezonansında olduğu gibi (devrenin aktif direncini ihmal edersek) eşitlikle belirlenir:

ωL = 1 / ω° C

Öyleyse:

er = 1 / 2π√LC

Lres = 1 / ω2C

Adet = 1 / ω2L

Bu üç nicelikten herhangi birini değiştirerek Xl = X° C eşitliği elde edilebilir, yani devreyi salınımlı bir devreye dönüştürün.

Yani, elektriksel salınımları indükleyebileceğimiz kapalı bir salınım devremiz var, yani. alternatif akım. Ve her salınımlı devrenin sahip olduğu aktif direnç olmasaydı, içinde sürekli olarak bir alternatif akım bulunabilirdi.Aktif direncin varlığı, devredeki salınımların kademeli olarak azalmasına ve bunları sürdürmek için bir enerji kaynağına - bir alternatöre ihtiyaç duyulmasına neden olur.

Sinüzoidal olmayan akım devrelerinde, çeşitli harmonik bileşenler için rezonans modları mümkündür.

Rezonans akımları pratikte yaygın olarak kullanılmaktadır. Akım rezonansı fenomeni, bant geçiren filtrelerde belirli bir frekansı geciktiren elektriksel bir "kelepçe" olarak kullanılır. f frekansında önemli bir akım direnci olduğu için, f frekansında devredeki gerilim düşümü maksimum olacaktır. Döngünün bu özelliğine seçicilik denir, radyo alıcılarında belirli bir radyo istasyonunun sinyalini izole etmek için kullanılır. Rezonans akım modunda çalışan salınımlı bir devre, ana bileşenlerden biridir. elektronik jeneratörler.