AC devresinde aktif direnç ve indüktör

Yalnızca endüktif direnç içeren bir AC devresi düşünüldüğünde (makaleye bakın) "Alternatif akım devresindeki indüktör"), bu devrenin aktif direncinin sıfır olduğunu varsaydık.

Aslında, hem bobinin kendi teli hem de bağlantı telleri küçük ama aktif bir dirence sahiptir, bu nedenle devre kaçınılmaz olarak akım kaynağının enerjisini tüketir.

Bu nedenle, bir dış devrenin toplam direncini belirlerken, reaktif ve aktif dirençlerini toplamak gerekir. Ancak yapı olarak farklı olan bu iki direnci bir araya getirmek mümkün değildir.

Bu durumda devrenin alternatif akıma empedansı geometrik toplama ile bulunur.

Bir tarafı endüktif direncin değeri ve diğer tarafı aktif direncin değeri olan dik açılı bir üçgen (bkz. Şekil 1) oluşturulur. İstenen devre empedansı, üçgenin üçüncü tarafı tarafından belirlenir.

Şekil 1. Endüktif ve aktif direnç içeren bir devrenin empedansının belirlenmesi

Devre empedansı Latin harfi Z ile gösterilir ve ohm cinsinden ölçülür. Toplam direncin her zaman ayrı ayrı alınan endüktif ve aktif dirençten daha büyük olduğu yapıdan görülebilir.

Toplam devre direnci için cebirsel ifade şu şekildedir:

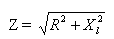
burada Z — toplam direnç, R — aktif direnç, XL — devrenin endüktif direnci.

Bu nedenle, aktif ve endüktif dirençten oluşan bir devrenin alternatif akıma karşı toplam direnci, bu devrenin aktif ve endüktif direncinin karelerinin toplamının kareköküne eşittir.

Ohm Yasası çünkü böyle bir devre I = U / Z formülüyle ifade edilir, burada Z devrenin toplam direncidir.

Şimdi devre, akım ve endüktans arasındaki faz kaymasına ek olarak nispeten büyük bir aktif dirence sahipse voltajın ne olacağını analiz edelim. Pratikte böyle bir devre, örneğin ince bir tel (yüksek frekans bobini) ile sarılmış demir çekirdekli bir indüktör içeren bir devre olabilir.

Bu durumda, akım ve gerilim arasındaki faz kayması artık çeyrek periyot (yalnızca endüktif dirençli bir devrede olduğu gibi) değil, çok daha az olacaktır; ve direnç ne kadar büyük olursa, faz kayması o kadar az olur.

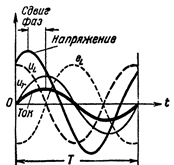
Şekil 2. R ve L içeren bir devrede akım ve gerilim.

Şimdi kendisi kendi kendine indüksiyonun EMF'si gerilime göre yarım periyot değil, daha az dengelendiği için akım kaynağı gerilimi ile anti-fazda değildir.Ek olarak, bobin terminallerinde akım kaynağı tarafından oluşturulan voltaj, kendi kendine endüksiyonun emf'sine eşit değildir, ancak bobin telinin aktif direncindeki voltaj düşüşü miktarından daha fazladır. Başka bir deyişle, bobindeki voltaj zaten iki bileşenden oluşur:

• tiL- EMF'nin etkisini kendi kendine endüksiyondan dengeleyen voltajın reaktif bileşeni,

• tiR- devrenin aktif direncinin üstesinden gelecek voltajın aktif bileşeni.

Eğer bobine seri olarak büyük bir aktif direnç bağlarsak faz kayması o kadar azalacaktır ki akım sinüs dalgası neredeyse gerilim sinüs dalgasına yetişecek ve aralarındaki faz farkı zar zor farkedilecektir.Bu durumda, terimin genliği ve terimin genliğinden daha büyük olacaktır.

Benzer şekilde, jeneratörün frekansını bir şekilde düşürürseniz, faz kaymasını azaltabilir ve hatta tamamen sıfıra düşürebilirsiniz. Frekanstaki bir azalma, kendi kendine endüksiyon EMF'sinde bir azalmaya ve dolayısıyla devrede neden olduğu akım ve voltaj arasındaki faz kaymasında bir azalmaya neden olacaktır.

Bir indüktör içeren bir AC devresinin gücü

Bobin içeren alternatif akım devresi, akım kaynağının enerjisini tüketmez ve devrede jeneratör ile devre arasında bir enerji alışverişi süreci vardır.

Şimdi böyle bir şema tarafından tüketilen güçle işlerin nasıl olacağını analiz edelim.

Bir AC devresinde tüketilen güç, akım ve voltajın ürününe eşittir, ancak akım ve voltaj değişken büyüklükler olduğundan, güç de değişken olacaktır.Bu durumda, akım değerini zamanın belirli bir anına karşılık gelen gerilim değeri ile çarparsak, zaman içindeki her an için güç değerini belirleyebiliriz.

Güç grafiğini elde etmek için farklı zamanlarda akım ve gerilimi tanımlayan doğru parçalarının değerlerini çarpmamız gerekir. Böyle bir yapı, Şek. 3 A. Kesikli dalga biçimi p, yalnızca endüktif direnç içeren bir AC devresinde gücün nasıl değiştiğini gösterir.

Bu eğrinin oluşturulmasında aşağıdaki cebirsel çarpma kuralı kullanılmıştır: Pozitif bir değer negatif bir değerle çarpıldığında negatif bir değer elde edilir ve iki negatif veya iki pozitif değer çarpıldığında pozitif bir değer elde edilir.

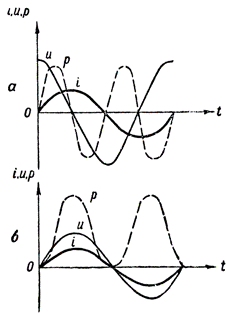
Şekil 3. Güç grafikleri: a — endüktif direnç içeren bir devrede, b — ayrıca aktif direnç

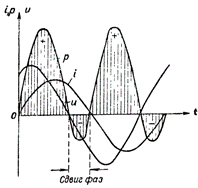
Şekil 4. R ve L içeren bir devre için güç grafiği.

Bu durumda güç eğrisi, zaman ekseninin üzerinde yer alır. Bu, jeneratör ile devre arasında enerji alışverişi olmadığı ve bu nedenle jeneratörün devreye verdiği gücün tamamen devre tarafından tüketildiği anlamına gelir.

İncirde. Şekil 4, hem endüktif hem de aktif direnç içeren bir devre için güç grafiğini göstermektedir. Bu durumda, devreden akım kaynağına ters enerji transferi de gerçekleşir, ancak bu, tek bir endüktif dirençli devreden çok daha az bir ölçüde gerçekleşir.

Yukarıdaki güç grafiklerini inceledikten sonra, devrede yalnızca akım ve gerilim arasındaki faz kaymasının "negatif" güç oluşturduğu sonucuna varıyoruz.Bu durumda, devredeki akım ve gerilim arasındaki faz kayması ne kadar büyük olursa devre tarafından o kadar az güç tüketilir ve tersine faz kayması ne kadar küçük olursa devre tarafından tüketilen güç o kadar büyük olur.

Ayrıca okuyun: voltaj rezonansı nedir