Gerilim, direnç ve güç üçgenleri

Vektör diyagramları hakkında bir fikri olan herkes, dik açılı bir voltaj üçgeninin üzerlerinde çok net bir şekilde ayırt edilebileceğini kolayca fark edecektir, bunların her biri şunları yansıtır: devrenin toplam voltajı, aktif direncin voltajı ve voltaj reaktansta.

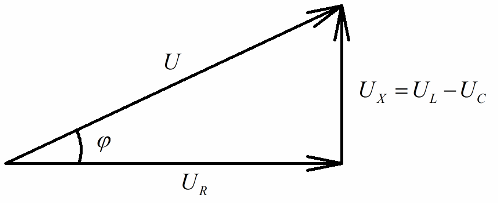
Pisagor teoremine göre, bu voltajlar arasındaki ilişki (devrenin toplam voltajı ile bölümlerinin voltajı arasındaki) şöyle görünecektir:

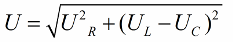
Bir sonraki adım, bu voltajların değerlerini akıma bölmekse (akım, seri devrenin tüm bölümlerinden eşit olarak akar), o zaman Ohm Yasası direnç değerlerini alıyoruz, yani artık dik açılı bir direnç üçgeninden bahsedebiliriz:

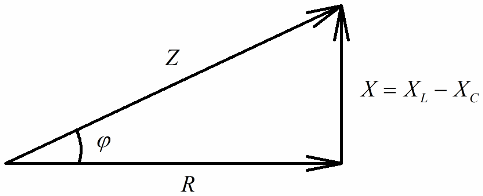
Benzer bir şekilde (gerilimlerde olduğu gibi), Pisagor teoremini kullanarak devrenin empedansı ile reaktanslar arasında bir ilişki kurmak mümkündür. İlişki aşağıdaki formülle ifade edilecektir:

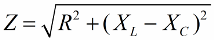
Daha sonra direnç değerlerini akımla çarparız, aslında dik üçgenin her iki tarafını da belirli sayıda artırmış oluruz. Sonuç olarak, kapasiteleri olan dik açılı bir üçgen elde ederiz:

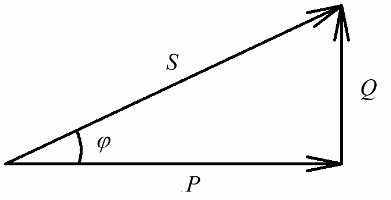
Elektrik enerjisinin (tesisattaki işlerin performansında ısıya) geri döndürülemez dönüşümü ile ilişkili devrenin aktif direncinde salınan aktif güç, enerjinin geri dönüşümlü dönüşümünde (yaratılış) yer alan reaktif güç ile açıkça ilişkili olacaktır. bobinler ve kapasitörlerdeki manyetik ve elektrik alanların) ve elektrik tesisatına tam güç sağlandığında.

Aktif güç watt (W), reaktif güç - varis cinsinden (VAR - volt-amper reaktif), toplam - VA (volt-amper) cinsinden ölçülür.

Pisagor teoremine göre şunu yazabiliriz:

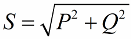
Şimdi, güç üçgeninde, kosinüsü öncelikle aktif güç ve görünür güç ile kolayca belirlenebilen bir phi açısı olduğu gerçeğine dikkat edelim. Bu açının kosinüsü (cos phi) güç faktörü denir. Bir elektrik tesisatında faydalı işler yapılırken toplam gücün ne kadarının hesaba katıldığını ve şebekeye geri verilmediğini gösterir.

Açıkçası, daha yüksek bir güç faktörü (maksimum bir), işletme için tesise iletilen enerjinin daha yüksek bir dönüşüm verimliliğini gösterir. Güç faktörü 1 ise, sağlanan tüm enerji iş yapmak için kullanılır.

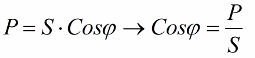
Elde edilen oranlar, tesisin mevcut tüketiminin güç faktörü, aktif güç ve şebeke voltajı cinsinden ifade edilmesini sağlar:

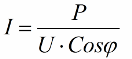
Yani, kosinüs phi ne kadar küçük olursa, ağın belirli bir işi yapması için o kadar fazla akım gerekir. Uygulamada, bu faktör (maksimum ağ akımı) iletim hattının iletim kapasitesini sınırlar ve bu nedenle, güç faktörü ne kadar düşükse, hat yükü o kadar büyük ve faydalı bant genişliği o kadar düşük olur (düşük kosinüs phi kısıtlamaya yol açar). Kosinüs phi'si azalan elektrik hatlarındaki joule kayıpları aşağıdaki formülden görülebilir:

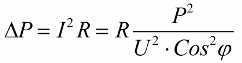
İletim hattının aktif direnci R'de, yüke reaktif olmasına rağmen akım I yükseldikçe kayıplar artar. Bu nedenle, düşük bir güç faktörü ile elektrik iletim maliyetinin arttığını söyleyebiliriz. Bu, kosinüs phi'yi artırmanın önemli bir ulusal ekonomik görev olduğu anlamına gelir.

Toplam gücün reaktif bileşeninin sıfıra yaklaşması istenir, bunun için elektrik motorlarını ve trafoları her zaman tam yükte kullanmak ve kullanım sonunda boşta kalmamaları için kapatmak iyi olur. Yüksüz durumda, motorlar ve transformatörler çok düşük bir güç faktörüne sahiptir. Kullanıcılarda kosinüs phi'yi artırmanın bir yolu kullanmaktır. kapasitör bankları Ve senkron kompansatörler.